去年看对称加密算法写的一些文档,补了几个坑,剩下的坑有空再补(咕咕咕
对称加密算法
对称密钥算法(英语:Symmetric-key algorithm)又称为对称加密、私钥加密、共享密钥加密,是密码学中的一类加密算法。这类算法在加密和解密时使用相同的密钥,或是使用两个可以简单地相互推算的密钥。算法安全性依赖于加密算法强度以及密钥的保密。
常见的对称加密算法有DES、3DES、AES、SM4、Blowfish、IDEA、TEA、RC4、RC5、RC6。对称加密的速度比公钥加密快很多,在很多场合都需要对称加密。
DES、3DES
关于DES
DES(Data Encryption Standard),是一种对称密钥块密码算法,分组大小为64位,密钥长度为56位(长度总共为64位,实际为56位,第8、16、24、32、40、48、56、64位是校验位)
3DES(Triple Data Encryption Algorithm),相当于对每个数据块应用三次DES即(DES_encrypt(DES_decrypt(DES_encrypt(plainText)))
算法原理
IP表初始置换
64位明文通过IP初始置换表置换为L0(置换后的数据的前32位),R0(置换后的数据的后32位)
子密钥生成
通过PC1置换表将56位密钥置换位C0(置换后的数据的前28位),D0(置换后的数据的后32位)
将C0,D0分别循环位移(位移表固定{ 1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1})得到C1、D1
C1、D1合并,通过PC2置换表得到第一个子密钥K1
回到第二步继续循环,得到子密钥K2、K3、……、K16
迭代加密
f函数(16轮)
Ln = R(n - 1);
Rn = L(n - 1)⊕f(Rn-1,kn-1)
其中涉及到E盒扩展、S盒压缩
Rn通过E盒由32位扩展到48位,而后与子密钥异或
异或得到的48位分为8个6位分组,分别进入S1——S8替换压缩,S盒有8个,每个64位,输入数据为6位,输出数据为4位,得到8个4位分组,即将48位数据通过S盒压缩成32位
S盒压缩得到的32位数据通过P盒置换得到新的32位数据
P盒置换得到的32位数据与Ln异或得到Rn+1
回到f函数继续迭代15轮(总共16轮)
将L16和R16整体互换位置(第16轮结束后)并且合并得到64位数据
输出
将得到的64位数据通过IP逆置换表置换得到64位数据并输出,这就是密文了
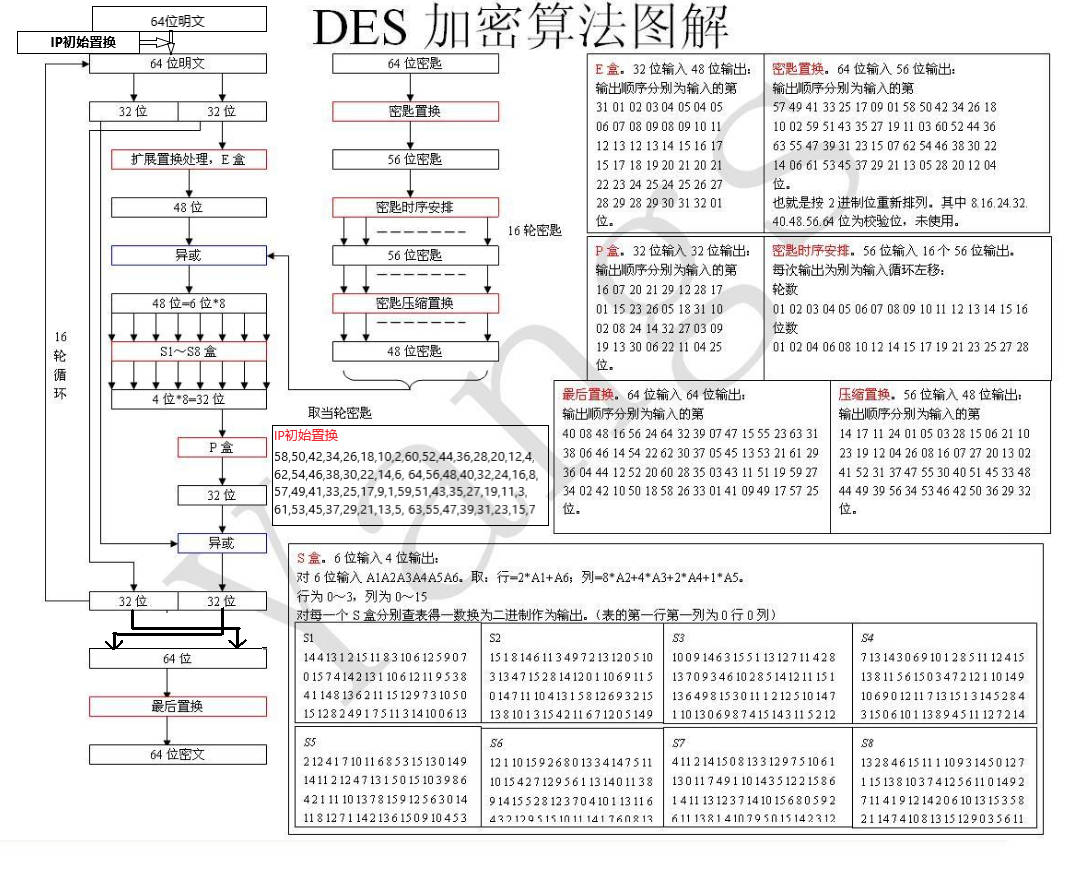
图解
图片来源于看雪会员Yangs的帖子,https://bbs.pediy.com/thread-90593.htm,我更正了少许错误
解密
解密过程与加密过程算法基本相同,唯一不同点的是子密钥要逆序使用,所以只要改变子密钥的顺序,逆序使用就可以得到明文了
DES加解密实现
C/C++实现
from https://cloud.tencent.com/developer/article/1016180
1 | //from https://cloud.tencent.com/developer/article/1016180 |
DES的扩展3-DES
3DES使用“密钥包”,其包含3个DES密钥,K1,K2和K3,均为56位(除去奇偶校验位)。加密算法为:
也就是说,使用K1为密钥进行DES加密,再用K2为密钥进行DES“解密”,最后以K3进行DES加密。
而解密则为其反过程:
即以K3解密,以K2“加密”,最后以K1解密。
每次加密操作都只处理64位数据,称为一块。
无论是加密还是解密,中间一步都是前后两步的逆。这种做法提高了使用密钥选项2时的算法强度,并在使用密钥选项3时与DES兼容。
- 密钥选项1:三个密钥是独立的。
- 密钥选项2:K1和K2是独立的,而K3=K1
- 密钥选项3:三个密钥均相等,即K1=K2=K3
AES
关于AES
AES(Advanced Encryption Standard),是一种对称密钥块密码算法,分组大小为128位,密钥长度为128,192或256位
算法原理
加解密实现
from https://github.com/dhuertas/AES
1 | /* |
IDEA
关于IDEA
国际数据加密算法(IDEA)是来学嘉与James Massey联合提出的。这种算法是在DES算法的基础上发展出来的,类似于三重DES。分组长度为64位,密钥长度为128位,算法使用3种不同代数群操作。
算法原理
子密钥生成
IDEA密钥长度为128位,子密钥长度为16位共52个
a.128位密钥分为8个16位分组,直接作为前八个子密钥
b.128位密钥循环左移25位,生成的128位密钥分为8个16位分组,作为接下来的8个子密钥
c.继续执行步骤b,直至52个子密钥全部生成完毕
IDEA加密
64为明文被分成4个16位分组。每一轮加密都需要6个子密钥,最后的输出变换只需要4个子密钥,所以共需8*6+4=52个子密钥。一轮加密中,4个16位子密钥分别通过2个模2^16+1(65537)乘法和2个模2^16(65536)加法运算与明文混合,并用2个16位子密钥按位异或对结果进行处理,前一轮加密结果作为后一轮加密的输入。总共进行8轮加密,最后用4个子密钥变换输出最终的密文。
IDEA解密
解密过程同加密过程,唯一不同的是子密钥不同。
解密所需的52个子密钥是加密子密钥相对于不同操作运输的逆元,且解密时子密钥使用顺序相反。(乘法逆元可以通过扩展欧几里得算法求出)
加解密实现
1 | // https://github.com/razvanalex/IDEA-encryption-algorithm |
SM4
关于SM4
SM4是一个具有128块大小和128位密钥的分组密码算法。加密算法和密钥扩展算法采用32轮线性非迭代结构,S盒输入为8bits,输出也为8bits。
算法原理
前置知识
F函数
F(X0, X1, X2, X3, rk) = X0 ⊕ T(X1 ⊕ X2 ⊕ X3 ⊕ rk)
合成置换T
由非线性变换τ 和线性变换L复合合成 T(x)=L(τ(x))
非线性变换τ
τ由四个并行的S-box组成(S-box为16*16 * 8bits,输入8bits,输出8bits)
若输出为A(A0, A1, A2, A3),输出为B(B0, B1, B2, B3)
则B(B0, B1, B2, B3) = τ(A) = (S-box(A0), S-box(A1), S-box(A2), S-box(A3)
线性变换L
线性变换L的输入是非线性变换τ的输出
输出C = L(B) = B ⊕ (B <<< 2) ⊕ (B <<< 10) ⊕ (B <<< 18) ⊕ (B <<< 24)
T’变换
T’(x)=L’(τ(x))
L’变换
C = L(B) = B ⊕ (B <<< 13) ⊕ (B <<< 23)
反序变换R(A0, A1, A2, A3) = (A3, A2, A1, A0)
密钥扩展算法
加密密钥128位为 MK(MK0, MK1, MK2, MK3)
子密钥128位,共32个为rk0, rk1 , … , rk31
系统参数FKi取值为FK[4] = {0xa3b1bac6, 0x56aa3350, 0x677d9197, 0xb27022dc}
固定参数CKi取值为 CK[32] = {
0x00070e15, 0x1c232a31, 0x383f464d, 0x545b6269, 0x70777e85, 0x8c939aa1,
0xa8afb6bd, 0xc4cbd2d9, 0xe0e7eef5, 0xfc030a11, 0x181f262d, 0x343b4249,
0x50575e65, 0x6c737a81, 0x888f969d, 0xa4abb2b9, 0xc0c7ced5, 0xdce3eaf1,
0xf8ff060d, 0x141b2229, 0x30373e45, 0x4c535a61, 0x686f767d, 0x848b9299,
0xa0a7aeb5, 0xbcc3cad1, 0xd8dfe6ed, 0xf4fb0209, 0x10171e25, 0x2c333a41,
0x484f565d, 0x646b7279};
子密钥生成算法如下
(K0,K1,K2,K3)=(MK0 ⊕ FK0, MK1⊕FK1, MK2⊕FK2, MK3⊕FK3)
rki = K(i+4) = Ki ⊕ T’(K(i+1) ⊕ K(i+2) ⊕ K(i+3) ⊕ CKi) (i = 0 ,1 , … , 31)
加密算法
明文输入为X(X0, X1, X2, X3),密文输出为Y(Y0, Y1, Y2, Y3)
Xi+4 = F(Xi, Xi+1, Xi+2, Xi+3, rki) = Xi ⊕ T(Xi+1 ⊕ Xi+2 ⊕ Xi+3 ⊕ rki) (i = 0 ,1 , … , 31)
Y(Y0, Y1, Y2, Y3) = R(X32, X33, X34, X35) = (X35, X34, X33, X32)
解密算法
解密算法和加密算法相同,唯一区别是密钥使用顺序要逆序使用
加解密实现
from https://zhuanlan.zhihu.com/p/43951432
sm4.c
1 | /************************************************************************* |
sm4.h
1 | /************************************************************************* |
sm4_code.c
1 | /************************************************************************* |
BlowFish
关于BlowFish算法
BlowFish是一个具有64位块大小和可变密钥长度(32位到448位)的分组密码算法。它是一个16轮Feistel密码,使用大型密钥相关的S盒。
算法原理
子密钥生成
子密钥生成使用了由18个32位字组成的P数组
4个8*32的包含1024个32位字的S-box
1 | uint32_t P[18]; |
步骤:
1.按顺序使用常数Π的小数部分初始化P数组和S-box
2.对P数组和密钥进行逐位异或,必要时重用密钥
3.使用当前的P数组和S-box对全0的64位分组使用BlowFish算法进行加密,用输出代替P[1]、P[2]
4.重复以上步骤使用当前的P数组和S-box对上一步输出进行加密,并用输出代替P[3]、P[4],直到按顺序替代所有的P数组和S-box中的元素为止
加密
f函数输入是一个32位双字,共4个字节,分别作为4个S-box的索引,取出相应的S-box的值然后进行模2^32加运算
1 | F(x) = F(a, b, c, d) = ((S1[a] + S2[b]) ^ S3[c]) + S4[d] |
加密是由16轮的Feistel网络组成
1 | void encrypt (uint32_t & L, uint32_t & R) { |
解密
解密方法与加密方法相同,只是P数组要逆序使用
1 | void decrypt (uint32_t & L, uint32_t & R) { |
加解密实现
1 | // create by feng on August 1, 2019 |
TEA、XTEA、XXTEA
关于TEA系列算法
微型加密算法(Tiny Encryption Algorithm,TEA)是一种易于描述和执行的块密码,通常只需要很少的代码就可实现。其设计者是David Wheeler、Roger Needham
TEA的分组长度为64位,密钥长度为128位,采用Feistel网络,建议32次循环加密即64轮
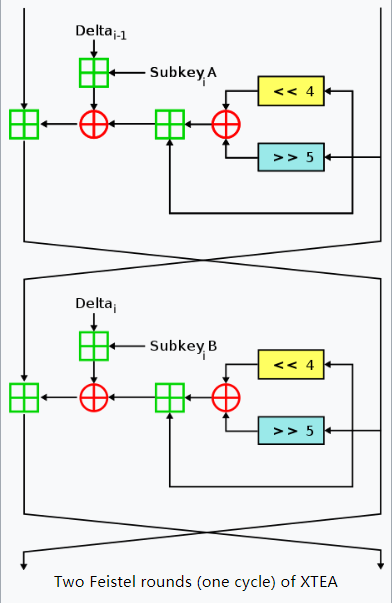
XTEA是TEA的扩展,同样是一个64位块的Feistel密码,使用128位密钥,建议64轮
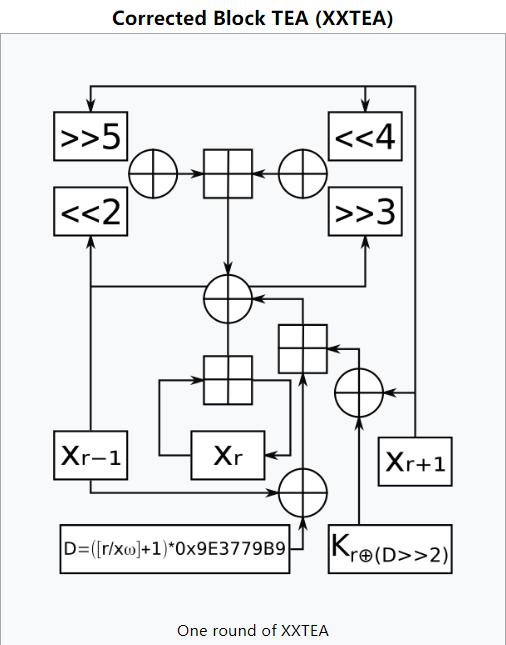
XXTEA是一个非平衡Feistel网络分组密码,在可变长度块上运行,这些块是32位大小的任意倍数(最小64位),使用128位密钥
TEA系列算法典型特征是采用密钥调度常数0x9e3779b9
加解密实现
TEA加解密实现
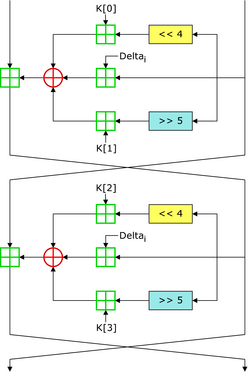
1 |
|
XTEA加解密实现
1 |
|
XXTEA加解密实现
1 |
|
XXTEA逆向分析
文件来源:2019RCTF babyre
该题大致为输入一个16位字符串经过多次变换最终输出Bingo! 即可,由于题目的原因出现多解,故还需满足md5(rctf{flag})==5f8243a662cf71bf31d2b2602638dc1d,此处不作解释,由于主要是讲解XXTEA的逆向分析,其他过程暂且不细说,我们看到其中最关键的加密函数sub_55A0DF892CE0。
1 | signed __int64 __fastcall sub_55A0DF892CE0(int *a1, signed int a2, __int64 a3) |
我们可以看到反编译的伪代码也是十分清晰的,纵观整个函数,整个函数过程都围绕着0x9E3779B9这个魔数,相信很多人都有似曾相识的感觉,没错!该函数与上文的XXTEA加解密实现结构基本相同,实现了XXTEA加解密。接下来我们看到函数的调用
1 | sub_55A0DF892CE0(v, -(v10 >> 2), key); // stea(v,-2,key) |
结合其他有关信息可以简单看出函数参数v为两个32位无符号数, -(v10 >> 2)的值为-2,key为128位密钥,它们是0xE0C7E0C7, 0xC6F1D3D7, 0xC6D3C6D3, 0xC4D0D2CE,此处调用了XXTEAdecode对两个32位无符号数进行解密,解密结果与之后的常量异或后比较判断
整个题目的核心算法就是XXTEA,只要识别出该算法,那么逆向将变得非常简单,逻辑无非就是输入一个16进制字符串之后hexencode,得到一个64位无符号数(即2个32位无符号数),然后将之2个32位无符号数xxteadecrypt得到新的64位无符号数,此处要求最后一个字节的值小于0x4,并将第(8-最后一个字节的值+1)字节的值置为00,而后将之经下一个函数进行一些位操作验证结果是否等于0x69e2,这一步并不改变原有值无视之,最终验证按字节与0x17异或出来结果是否为Bingo!,结合上面猜测第7字节的值为00,最后一个字节值为0x02,且md5(rctf{flag})==5f8243a662cf71bf31d2b2602638dc1d,由此可以确定最终解密后的64位无符号数的值为0x02XX367870797e55(小端序),直接写脚本就可以爆破次高8位即可,依次就可以得到该题的flag了
1 |
|
TX TEA魔改算法
TX 将TEA算法魔改成16轮(TEA保密的最低要求)并且广泛应用
相关内容可以看这里腾讯TEA加密算法
主要就是将加密轮次改为16轮,并且采用改进的CBC模式加密
总结
对于TEA系列算法的识别只要依据常数0x9e3779b9并且其相关加密结构就可以很容易判断是TEA、XTEA亦或XXTEA,之后只要找到其密文以及加密密钥辅以以上加解密实现代码就可以很快解密了,TEA算法在逆向分析中,IDA反编译以后一般都是比较清晰的,只要有一定的了解就能轻而易举的识别出对应算法,而后动态调试验证即可,至于findcrypto3插件识别也是依据常数识别的,所以只要知道这个特征即可。
附件
参考文献
RC4
关于RC4算法
RC4(Rivest Cipher 4)是一种流加密算法,密钥长度可变。加解密使用相同的密钥,美国密码学家Ronald Rivest在1987年设计的。
RC4由伪随机数生成器和异或运算组成。密钥长度可变,范围是[1,255]。RC4一个字节一个字节地加解密。给定一个密钥,伪随机数生成器接受密钥并产生一个S盒。S盒用来加密数据,而且在加密过程中S盒会变化。
由于异或运算的对合性,RC4加密解密使用同一套算法。
加解密实现
伪代码
KSA(the Key-Scheduling Algorithm)
通过密钥调度算法(KSA)初始化长度为256的S盒。第一个for循环将0到255的互不重复的元素装入S盒。第二个for循环根据密钥打乱S盒。
1 | for i from 0 to 255 |
PGRA(the Pseudo-Random Generation Algorithm)
下面i,j是两个指针。每收到一个字节,就进行while循环。通过一定的算法((a),(b))定位S盒中的一个元素,并与输入字节异或,得到k。循环中还改变了S盒((c))。如果输入的是明文,输出的就是密文;如果输入的是密文,输出的就是明文。
1 | i := 0 |
C语言实现
1 |
|
逆向分析
RC4反汇编/反编译之后一般有两个函数,一个就是用key初始Sbox,另外一个就是按字节加密字符串,以下两个函数是RC4加密反编译的结果
1 | unsigned __int64 __fastcall RC4_init(__int64 a1, __int64 a2, int a3) |
1 | __int64 __fastcall RC4(__int64 a1, __int64 a2, __int64 a3, int a4, int a5) |
用伪随机数数列初始化Sbox是其最大的特征,另外一个特征就是无论是初始化Sbox还是加密过程都大量用到unsigned __int8也就是加密过程中的mod256,有一些可执行文件反编译之后就直接是mod256,这更好判断,一般RC4题型都是结合base64encode等其他编码方法出题的,解密只要找到key和加密后的字符串利用以上代码解密即可
hash算法
MD5
关于MD5
MD5消息摘要算法,一种被广泛使用的密码散列函数,可以产生出一个128位(16字节)的散列值(hash value),用于确保信息传输完整一致。
算法原理
数据填充
填充消息使其长度与448模512同余,即使长度满足要求也需填充,填充方法是:附加一个1在消息后面,然后用0填充,直到消息长度与448模512同余,至少填充1位,至多填充512位
添加长度
在第一步的结果之后附加上64位的消息长度,若消息长度大于2^64则只记录其低64位,附加之后消息长度正好是512的倍数
初始化变量
A=0X67452301L,B=0XEFCDAB89L,C=0X98BADCFEL,D=0X10325476L
4.处理分组数据并输出
以512位一一个分组由类似的64次循环构成,分成4组16次。F 一个非线性函数;一个函数运算一次。Mi 表示一个 32-bits 的输入数据,Ki表示一个 32-bits 常数,用来完成每次不同的计算。
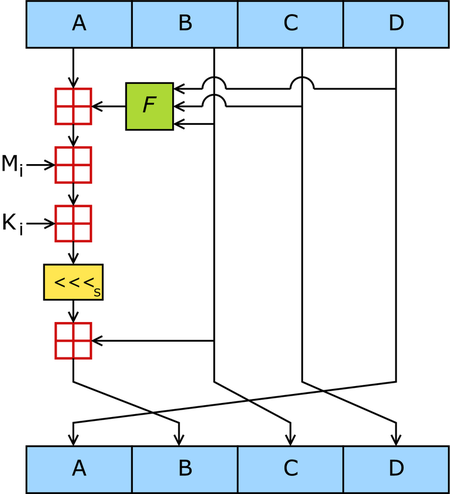
四个非线性函数为
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
待到所有分组处理完毕后输出一个128bit的散列结果
伪代码(from wiki)
1 | //Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating |
C语言实现
from https://github.com/pod32g/MD5
1 | // from https://github.com/pod32g/MD5 |
md5逆向分析
逆向分析中如果软件采用openssl等加密库载入od、ida显而易见就可知是md5加密,而对于一些原生的c、c++等语言实现的md5加密算法,也可以通过md5初始化变量这个特征来实现,下面是一个md5加密过程反汇编的结果
1 | push ebp |
显而易见程序初始化了4个变量,恰好是A=0X67452301L,B=0XEFCDAB89L,C=0X98BADCFEL,D=0X10325476L,据此可以初步识别为md5算法,继续向下追踪明文填充、分组处理进而可以判断加密过程是否为md5算法。
对于 md5(input) == 常量一般只能通过诸如爆破的方法求出input,而更多的软件一般都是采用 md5(input) == sn对此破解即变得相当简单,简单分析是否为md5变种亦或是对sn还采取了其他算法加密、编码,就可以依此来编写注册机。
md5穷举
md5算法本身不可逆,解密都是基于彩虹表(cmd5)、暴力破解工具(hashcat)、以及字典
cmd5(cmd5实时查询已收录11位及11位以下数字,8位小写字母,7位小写字母加数字,1-6位大小写字母+数字+特殊字符)
md5碰撞
2004年,王小云教授提出了非常高效的MD5碰撞方法。
2009年,冯登国、谢涛利用差分攻击,将MD5的碰撞算法复杂度进一步降低。
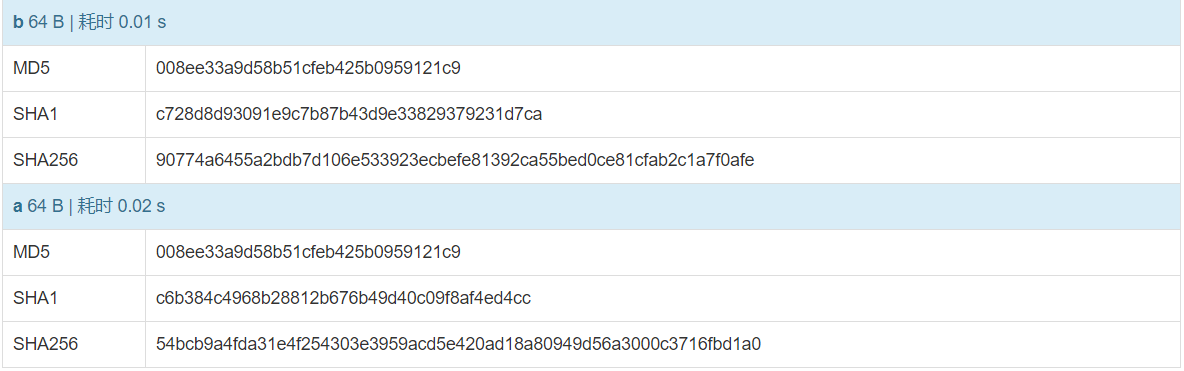
以下是一个md5碰撞的例子
文件a二进制为
1 | 4DC968FF0EE35C209572D4777B721587D36FA7B21BDC56B74A3DC0783E7B9518AFBFA200A8284BF36E8E4B55B35F427593D849676DA0D1555D8360FB5F07FEA2 |
文件b二进制为
1 | 4DC968FF0EE35C209572D4777B721587D36FA7B21BDC56B74A3DC0783E7B9518AFBFA202A8284BF36E8E4B55B35F427593D849676DA0D1D55D8360FB5F07FEA2 |
两个文件都具有共同的md5值008ee33a9d58b51cfeb425b0959121c9
总结
MD5算法已经不具备安全性,不应将之运用于密码存储、软件加解密等应用上,当然在当前,MD5算法因其普遍、稳定、快速的特点,仍广泛应用于普通数据的错误检查领域。